Advertisements
Advertisements
Question
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
Solution
Given:
A = B = 60° .....(1)
To verify:
sin (A − B) = sin A cos B − cos A sin B ......(2)
Now consider LHS of the expression to be verified in equation (2)
Therefore,
`sin (A - B) = sin (B - B)`
= sin 0
= 0
Now by substituting the value of A and B from equation (1) in the above expression
We get,
`sinAcosB - cosAsinB = sin B cosB - cosBsinB`
= 0
Hence it is verified that,
sin (A − B) = sin A cos B − cos A sin B
APPEARS IN
RELATED QUESTIONS
if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
Evaluate:
sin600 cos300 + cos600 sin300
From the following figure, find the values of:
- sin A
- cos A
- cot A
- sec C
- cosec C
- tan C

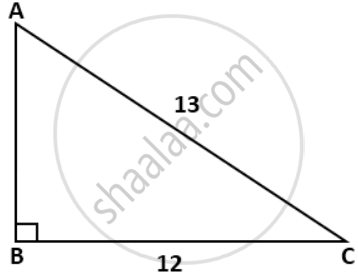
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
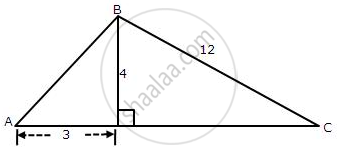
From the following figure, find the values of
(i) sin B
(ii) tan C
(iii) sec2 B - tan2B
(iv) sin2C + cos2C
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: cos C
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: `("cos A" - "sin A")/("cos A" + "sin A")`