Advertisements
Advertisements
प्रश्न
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
उत्तर
Given:
A = B = 60° .....(1)
To verify:
sin (A − B) = sin A cos B − cos A sin B ......(2)
Now consider LHS of the expression to be verified in equation (2)
Therefore,
`sin (A - B) = sin (B - B)`
= sin 0
= 0
Now by substituting the value of A and B from equation (1) in the above expression
We get,
`sinAcosB - cosAsinB = sin B cosB - cosBsinB`
= 0
Hence it is verified that,
sin (A − B) = sin A cos B − cos A sin B
APPEARS IN
संबंधित प्रश्न
If A = 30° B = 60° verify Sin (A + B) = Sin A Cos B + cos A sin B
If A and B are acute angles such that tan A = 1/2, tan B = 1/3 and tan (A + B) = `(tan A + tan B)/(1- tan A tan B)` A + B = ?
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
If A = 300 , verify that:
(i) sin 2A = `(2 tan A)/(1+tan^2A)`
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
tan 30° × tan ______° = 1
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
From the given figure, find the values of sin B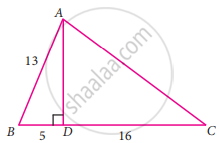
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
