Advertisements
Advertisements
Question
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
Solution
sin θ = `(8)/(17) = "Perpendicular"/"Hypotenuse"`
Base
= `sqrt(("Hypotenuse")^2 - ("Perpendicular")^2`
= `sqrt(17^2 - 8^2)`
= `sqrt(225)`
= 15
cos θ = `"Base"/"Hypotenuse" = (15)/(17)`
tan θ = `"Perpendicular"/"Base" = (8)/(15)`
cosecθ = `(1)/"sin θ" = (17)/(8)`
sec θ = `(1)/"cos θ " = (17)/(15)`
cot θ = `(1)/"tan θ " = (15)/(8)`.
APPEARS IN
RELATED QUESTIONS
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P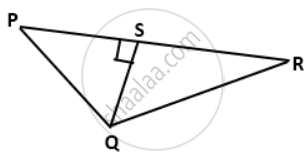
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
