Advertisements
Advertisements
Question
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

Solution 1
Consider the given figure :
Since the triangle is a right-angled triangle, so using Pythagorean Theorem
AC2 = 52 + 122
AC2 = 25 + 144 + 169
AC = 13
In ΔCBD and ΔCBA, the ∠C is common to both the triangles, ∠CDB = ∠CBA = 90° so therefore ∠CBD = ∠CAB.
Therefore ΔCBD and ΔCBA are similar triangles according to AAA Rule
So
`"AC"/"BC" = "AB"/"BD"`
`(13)/(5) = ( 12)/"BD"`
`"BD = (60)/(13)`
(i) cos ∠DBC = `"base"/"hypotenuse" = "BD"/"BC" = (60/13)/(5) =(12)/(13)`
(ii) cot ∠DBA =`"base"/"perpendicular" = "BD"/"AB" = (60/13)/(12) =(5)/(13)`
Solution 2
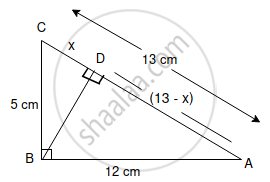
Since the triangle ABC is a right-angled triangle, so using Pythagorean Theorem,
AC2 = BC2 + AB2
AC2 = 52 + 122
AC2 = 25 + 144
AC2 = 169
AC2 = `sqrt169`
AC = 13
In ΔDBC, using Pythagorean Theorem,
BC2 = CD2 + BD2
(5)2 = x2 + BD2
25 - x2 = BD2
BD2 = 25 - x2 ...(i)
In ΔDBA, using Pythagorean Theorem,
BA2 = DA2 + BD2
(12)2 = (13 - x)2 + BD2
144 = (13 - x)2 + BD2
144 = 169 + x2 - 26x + BD2
144 - 169 - x2 + 26x = BD2
BD2 = - 25 - x2 + 26x ...(ii)
From equation (i) and (ii)
25 - x2 = - 25 - x2 + 26x
25 + 25 = 26x
x = `50/26`
x = `25/13`
In ΔBDC,
BC = 5 ; CD = `25/13`
BD2 = 25 - x2
= 25 - `(25/13)^2`
= 25 - `625/169`
= 25 `(1 - 25/169)`
= `25 ((169 - 25)/169)`
BD = `sqrt(25 (144/169))`
BD = `(5 xx 12)/13`
BD = `60/13`
In ΔDBA,
AB = 12; BD = `60/13`
AD = 13 - x
= `13 - 25/13 = (169 - 25)/13 = 144/13`
(i) cos ∠DBC = `"Base"/"hypotenuse" = (60/13)/5 = 60/65 = 12/13`
(ii) cot ∠DBA `= "Base"/"perpendicular" = (60/13)/(144/13) = 60/144 = 10/24 " i.e.," 5/13`
APPEARS IN
RELATED QUESTIONS
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
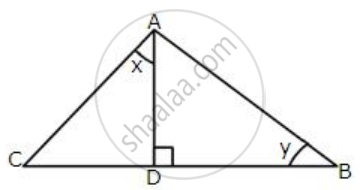
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
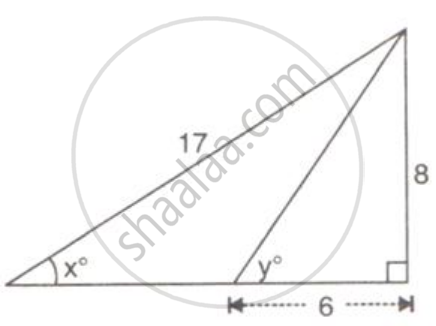
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosec C = `sqrt(10)`
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`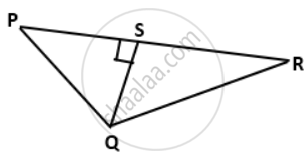
From the given figure, find the values of tan C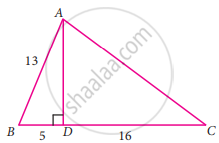
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
