Advertisements
Advertisements
Question
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
Solution
Here 20 + 45° and 30 – θ° are acute angles:
We know that (90 – θ) = cos θ
sin (2θ + 45°) = sin (90 – (30 – θ))
sin (2θ + 45°) = sin (90 – 30 + θ)
sin (20 + 45°) = sin (60 + θ)
On equating sin of angle of we get
2θ + 45 = 60 + θ
2θ – θ = 60 – 45
θ = 15°
APPEARS IN
RELATED QUESTIONS
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
Evaluate:
cos600 cos300− sin600 sin300
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
sin20° = cos ______°
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosec C = `sqrt(10)`
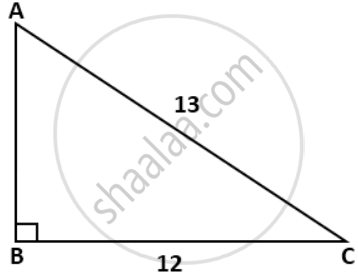
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: `("cos A" - "sin A")/("cos A" + "sin A")`