Advertisements
Advertisements
Question
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
Solution
3 `(x^2 -1/x^2)`
`=9/3(x^2 - 1/x^2)`
=`1/3 (9x^2-9/x^2)`
=`1/3 [(3x^2)-(3/x)^2]`
=`1/3 [(cosec theta )^2 - (cot theta)^2]`
=`1/3 ( cosec^2 theta - cot^2 theta)`
=`1/3 (1)=1/3`
APPEARS IN
RELATED QUESTIONS
If 8 tan A = 15, find sin A – cos A.
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
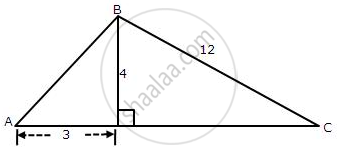
From the following figure, find the values of
(i) sin B
(ii) tan C
(iii) sec2 B - tan2B
(iv) sin2C + cos2C
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
If 5 cos = 6 sin ; evaluate:
(i) tan θ
(ii) `(12 sin θ – 3 cos θ)/(12 sin θ + 3 cos θ)`
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
