Advertisements
Advertisements
Question
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
Solution
A = 300
⇒ 2A = 2 × 300 = 600
By substituting the value of the given T-ratio, we get:
cos A = `sqrt((1+ cos^2A)/2)`
cos `30^0 = sqrt((1+cos 60^0)/2) = sqrt((1+(1/2)/2)) = sqrt((3/2)/2) =sqrt(3/4) = sqrt(3)/2`
∴ cos A = `sqrt(3)/2`
APPEARS IN
RELATED QUESTIONS
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
If cot θ = 2 find all the values of all T-ratios of θ .
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
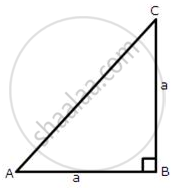
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A