Advertisements
Advertisements
Question
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
Solution
ΔPQR right angled at Q.
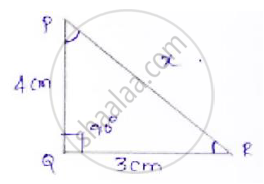
Let x be the hypotenuse
By applying Pythagoras
𝑃𝑅2 = 𝑃𝑄2 + 𝑄𝑅2
𝑥2 = 42 + 32
𝑥2 = 16 + 9
`∴ x = sqrt25 = 5`
Find sin 𝑃 , sin 𝑅, sec 𝑃, sec 𝑅
At LP, opposite side = 3 cm
Adjacent side = 4 cm
Hypotenuse = 5
`sin P = "𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑠𝑖𝑑𝑒"/"𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒" = 3/5`
`sec P = "𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒"/"𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑠𝑖𝑑𝑒" = 5/4`
At LK, opposite side = 4 cm
Adjacent side = 3 cm
Hypotenuse = 5 cm
`sin R = 4/5`
`sec R = 5/3`
APPEARS IN
RELATED QUESTIONS
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
If cot θ = `3/4` , show that `sqrt("sec θ - cosecθ"/"secθ + cosecθ" ) = 1/ sqrt(7)`
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
`(cos 28°)/(sin 62°)` = ?
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cosec C
