Advertisements
Advertisements
Question
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
Solution
Given
`A = 30^@ and B = 60^@`
To verify:
`cos(A + B) = cos A cos B - sinA sin B` ......(2)
Now consider LHS of the expression to be verified in equation (2)
Therefore,
`cos(30 + 60) = cos 90`
= 0
Now consider RHS of the expression to be verified in equation (2)
Therefore,
cosA cos B - sin A sin B = cos 30 cos 60 - sin 30 sin 60
`= sqrt3/2 xx 1/2 - 1/2 xx sqrt3/2`
= 0
Hence it is verfified that
cos (A + B) = cos A cos B - sin A sin B
APPEARS IN
RELATED QUESTIONS
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If A = 600 and B = 300, verify that:
(ii) cos (A – B) = cos A cos B + sin A sin B
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`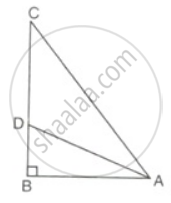
From the given figure, find the values of tan C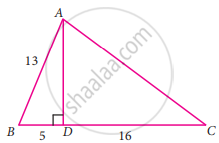
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
