Advertisements
Advertisements
Question
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
Solution
LHS=`(1-sin 60^0)/(cos 60^0) =(1-(sqrt(3))/2)/(1/2) = (((2-sqrt(3))/2))/(1/2) =((2-sqrt(3))/2) xx2=2-sqrt(3)`
RHS=`(tan60^0-1)/(tan60^0+1) = (sqrt(3)-1)/(sqrt(3)+1) = (sqrt(3)-1)/(sqrt(3)+1) xx(sqrt(3)-1)/(sqrt(3)+1)=((sqrt(3)-1)^2)/((sqrt(3))^2-1^2)=(3+1-2sqrt(3))/(3-1) =(4-2sqrt(3) )/2 = 2-sqrt(3)`
Hence, LHS = RHS
`∴ (1-sin 60^0)/(cos 60^0)=(tan 60^0-1)/(tan60^0+1)`
APPEARS IN
RELATED QUESTIONS
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ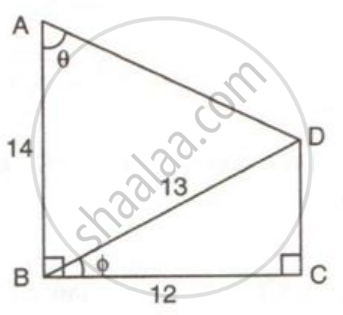
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
From the given figure, find the values of sin B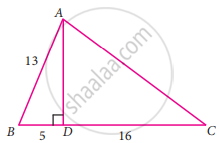
From the given figure, find the values of cosec C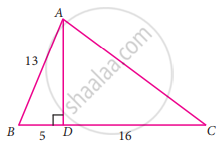
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
