Advertisements
Advertisements
Question
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
Solution
On substituting the values of various T-ratios, we get:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
=`4/(sqrt(3))^2 + 1/(1/2)^2 -2xx(1/sqrt(2))^2-(0)^2`
=`4/3 +1/(1/4) -2xx1/2-0`
=`4/3 +4-1`
=`4/3+3=(4+9)/3=13/3`
APPEARS IN
RELATED QUESTIONS
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
Prove that
cosec (65 °+ θ) sec (25° − θ) − tan (55° − θ) + cot (35° + θ) = 0
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A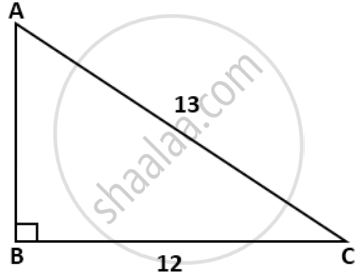
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
