Advertisements
Advertisements
Question
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
Solution
\[\begin{array}{l}\text{ L.H.S} = \sin( {50}^\circ + \theta) - \cos( {40}^\circ- \theta) + \tan 1^\circ \tan {10}^\circ \tan {80}^\circ \tan {89}^\circ \\ \end{array}\]
\[\begin{array}{l}= \sin{ {90}^\circ - ( {40}^\circ - \theta)} - \cos( {40}^\circ - \theta) + {\tan 1^\circ \tan( {90}^\circ - 1^\circ )}{\tan {10}^\circ \tan( {90}^\circ -{10}^{} )} \\ \end{array}\]
\[\begin{array}{l}= \cos( {40}^\circ - \theta)- \cos( {40}^\circ - \theta) + (\tan 1^\circ \cot 1^\circ )(\tan {10}^\circ \cot {10}^\circ ) \\ \end{array}\]
\[\begin{array}{l}= (\frac{1}{\cot 1^\circ } \times \cot 1^\circ )(\tan {10}^\circ \times \frac{1}{\tan {10}^0}) \\ \end{array}\]
\[\begin{array}{l}= 1 \times 1 \\ \end{array}\]
=RHS
APPEARS IN
RELATED QUESTIONS
If θ = 30° verify that `sin 2theta = (2 tan theta)/(1 + tan^2 theta)`
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
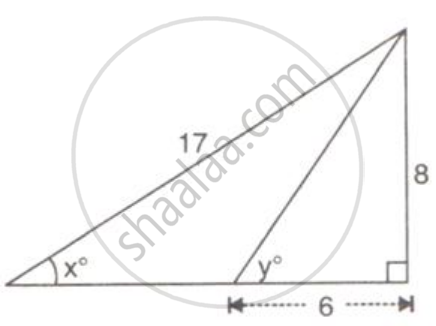
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`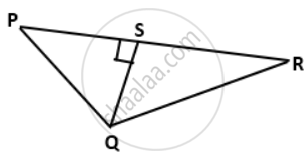
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y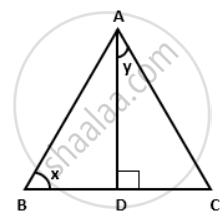
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
