Advertisements
Advertisements
Question
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
Solution
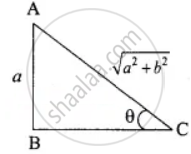
sin θ = `"a"/sqrt("a"^2 + "b"^2)`
In the triangle ΔABC
BC2 = AC2 – AB2
= `(sqrt("a"^2 + "b"^2))^2 - "a"^2`
= a2 + b2 − a2 = b2
BC = `sqrt("b"^2)` = b
cos θ = `"b"/sqrt("a"^2 + "b"^2)`
L.H.S = b sin θ
= `"b" "a"/sqrt("a"^2 + "b"^2)`
= `"ab"/sqrt("a"^2 + "b"^2)`
R.H.S = a cos θ
= `"a" "b"/sqrt("a"^2 + "b"^2)`
= `"ab"/sqrt("a"^2 + "b"^2)`
L. H. S = R. H. S
APPEARS IN
RELATED QUESTIONS
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
If sin A = `9/41` find all the values of cos A and tan A
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
Evaluate:
sin600 cos300 + cos600 sin300
cos 40° = sin ______°
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
