Advertisements
Advertisements
Question
If sin A = `9/41` find all the values of cos A and tan A
Solution
We have sin A = `9/41`
As,
`Cos^2 A= 1 − sin^2 A`
=`1-(9/41)^2`
=`1-81/1681`
=`(1681-81)/1681`
`⇒ cos^2 A = 1600/1681`
`⇒ cos A = sqrt(1600/1681)`
`⇒ cos A = 40/41`
Also,
`Tan A = sin A/cos A`
`= ((9/41))/((40/41))`
`=9/40`
APPEARS IN
RELATED QUESTIONS
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
If sin θ = `3/4` show that `sqrt((cosec^2theta - cot^2theta)/(sec^2theta-1)) =sqrt(7)/3`
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
If tan = 0.75, find the other trigonometric ratios for A.
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y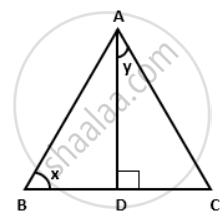
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
