Advertisements
Advertisements
Question
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ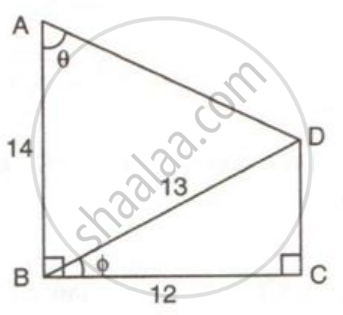
Solution
Consider the figure :
A perpendicular is drawn from D to the side AB at point E which makes BCDE is a rectangle.
Now in right-angled triangle BCD using Pythagorean Theorem
⇒ BD2 = BC2 + CD2 ...( AB is hypotenuse in ΔABD)
⇒ CD2 = 132 – 122 = 25
∴ CD = 5
Since BCDE is rectangle so ED 12 cm, EB = 5 and AE = 14 - 5 = 9
(i) sin Ø = `"CD"/"BD" = (5)/(13)`
tan θ = `"ED"/"AE" = (12)/(9) = (4)/(3)`
(ii) sec θ = `"AD"/"AE"`
sec θ = `"AD"/(9)`
AD = 9 secθ
Or
cosec θ = `"AD"/"ED"`
cosec θ = `"AD"/(12)`
AD = 12cosec θ
APPEARS IN
RELATED QUESTIONS
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
If θ = 30° verify `tan 2 theta = (2 tan theta)/(1 - tan^2 theta)`
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If A and B are acute angles such that tan A = 1/2, tan B = 1/3 and tan (A + B) = `(tan A + tan B)/(1- tan A tan B)` A + B = ?
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
Using the formula, sin A = `sqrt((1-cos 2A)/2) ` find the value of sin 300, it being given that cos 600 = `1/2`
tan 30° × tan ______° = 1
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
