Advertisements
Advertisements
प्रश्न
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ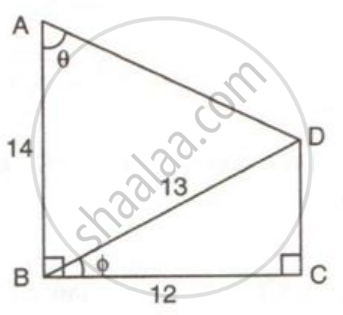
उत्तर
Consider the figure :
A perpendicular is drawn from D to the side AB at point E which makes BCDE is a rectangle.
Now in right-angled triangle BCD using Pythagorean Theorem
⇒ BD2 = BC2 + CD2 ...( AB is hypotenuse in ΔABD)
⇒ CD2 = 132 – 122 = 25
∴ CD = 5
Since BCDE is rectangle so ED 12 cm, EB = 5 and AE = 14 - 5 = 9
(i) sin Ø = `"CD"/"BD" = (5)/(13)`
tan θ = `"ED"/"AE" = (12)/(9) = (4)/(3)`
(ii) sec θ = `"AD"/"AE"`
sec θ = `"AD"/(9)`
AD = 9 secθ
Or
cosec θ = `"AD"/"ED"`
cosec θ = `"AD"/(12)`
AD = 12cosec θ
APPEARS IN
संबंधित प्रश्न
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
If cot θ= 1; find the value of: 5 tan2 θ+ 2 sin2 θ- 3
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos2 C + cosec2 C
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
