Advertisements
Advertisements
प्रश्न
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
उत्तर
Consider the diagram below :
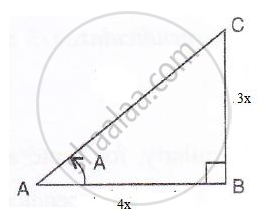
3cos A = 4 sin A
cot A = `(4)/(3)`
i.e. `"base"/"perpendicular" = (4)/(3) ⇒ "AB"/"BC" = (4)/(3)`
Therefore if length of AB = 4x, length of BC = 3x
Since
AB2 + BC = AC2 ...[ Using Pythagoras Theorem]
(4x)2 + (3x)2 = AC2
AC2 = 25x2
∴ AC = 5x ...( hypotenuse)
(i) cos A = `"AB"/"AC" = (4)/(5)`
(ii) cosec A = `"AC"/"BC" = (5)/(3)`
Therefore
3–cot2 A + cosec2 A
= `3 – (4/3)^2+(5/3)^2`
= `(27 – 16 + 25)/(9)`
=`(36)/(9)`
= 4
APPEARS IN
संबंधित प्रश्न
In right angled triangle ABC. ∠C = 90°, ∠B = 60°. AB = 15 units. Find remaining angles and sides.
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If cot θ = `3/4` , show that `sqrt("sec θ - cosecθ"/"secθ + cosecθ" ) = 1/ sqrt(7)`
In a right-angled triangle, it is given that A is an acute angle and tan A = `(5) /(12)`.
find the value of :
(i) cos A
(ii) sin A
(iii) ` (cosA+sinA)/(cosA– sin A)`
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
From the given figure, find the values of sin B