Advertisements
Advertisements
प्रश्न
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
उत्तर
Consider the diagram below :
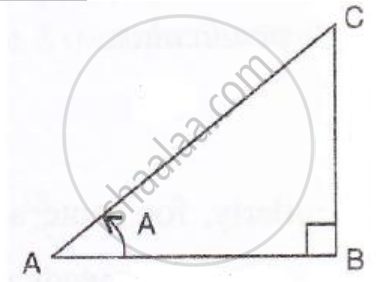
sec A =`sqrt2`
i.e.`"hypotenuse"/"base" =(sqrt2)/(1) ⇒ "AC"/"AB" =(sqrt2)/(1)`
Therefore if length of AB = x, length of AC =`sqrt2`
Since
AB2 + BC2 = AC2 ...[ Using Pythagoras Theorem]
(x)2 + BC2 = (`sqrt2"x")^2`
BC2 = 2x2 – x2 = x2
∴ BC = x ...(perpendicular)
Now
tan A = `"perpendicular"/"base" = ("x")/("x") =1`
sin A = `"perpendicular"/"hypotenuse" = ("x")/(sqrt2"x") = (1)/(sqrt2)`
cos A = `"base"/"hypotenuse" = ("x")/(sqrt2"x") = (1)/(sqrt2)`
Therefore
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
= `(3(1/sqrt2)^2+5(1)^2)/(4(1)^2 – (1/sqrt2)^2)`
= `(13/2)/(7/2)`
= `(13)/(7)`
=`1(6)/(7)`
APPEARS IN
संबंधित प्रश्न
Given 15 cot A = 8. Find sin A and sec A.
If θ = 30° verify `tan 2 theta = (2 tan theta)/(1 - tan^2 theta)`
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`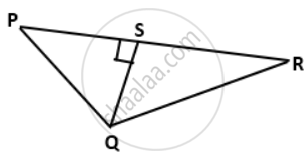
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
