Advertisements
Advertisements
प्रश्न
Given 15 cot A = 8. Find sin A and sec A.
उत्तर
Consider a right-angled triangle, right-angled at B.
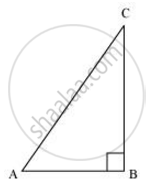
It is given that
cot A = `8/15`
`("AB")/("BC")=8/15`
Let AB be 8k.
Therefore, BC will be 15k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
= (8k)2 + (15k)2
= 64k2 + 225k2
= 289k2
AC = 17k
sin A = `(15k)/(17k)`
= `15/17`
sec A = `("AC")/("AB")`
= `17/8`
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
If 8 tan A = 15, find sin A – cos A.
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
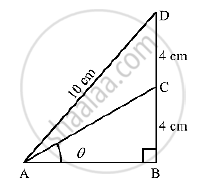
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
Evaluate:
`(sin^2 30^0 + 4 cot^2 45^0-sec^2 60^0)(cosec^2 45^0 sec^2 30^0)`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
cos 40° = sin ______°
If tan x = `1(1)/(3)`, find the value of : 4 sin2x - 3 cos2x + 2
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosec C = `sqrt(10)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: sinA
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: `("cos A" - "sin A")/("cos A" + "sin A")`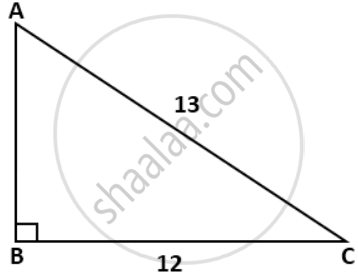
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
