Advertisements
Advertisements
प्रश्न
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
उत्तर
LHS = `((1-tan^2theta))/((1+tan^2theta))`
=` ((1-1/cot^2theta))/((1+1/cot^2theta))`
=`((cot^2theta-1)/(cot^2theta))/(((cot^2theta+1)/(cot^2theta)))`
=`(cot^2theta-1)/(cot^2theta+1)`
=`((4/3)^2-1)/((4/3)^2 +1)` (𝐴𝑠, 3 cot 𝜃 = 4 𝑜𝑟 cot 𝜃 =`4/3`)
=`(16/9-1)/(16/9+1)`
=`(((16-9)/9))/(((16+9)/9))`
=`((7/9))/((25/9))`
= `7/25`
𝑅𝐻𝑆 = `(cos^2 theta − sin^2 theta)`
=`((cos^2theta - sin^2 theta))/1`
=`(((cos^2theta-sin^2theta)/(sin^2theta)))/((1/(sin^2theta)))`
=`((cos^2theta)/(sin^2theta)-(sin^2theta)/(sin^2theta))/(cosec^2theta)`
=`((cot^2theta-1))/((cot^2theta+1))`
=`([(4/3)^2-1])/([(4/3)^2+1])`
=`((16/9-1/1))/((16/9+1/1))`
=`(((16-9)/9))/(((16+9)/9))`
=`((7/9))/((25/9))`
=`7/25`
Since, LHS = RHS
Hence, verified.
APPEARS IN
संबंधित प्रश्न
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
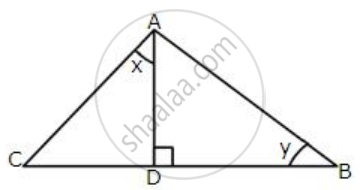
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cos A = `(7)/(25)`
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
