Advertisements
Advertisements
प्रश्न
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
उत्तर
It is given that sec 𝜃`=17/8`
Let us consider a right ΔABC right angled at B and ∠𝐶 = 𝜃
We know that cos 𝜃 =`1/sectheta = 8/17 =(BC)/(AC)`
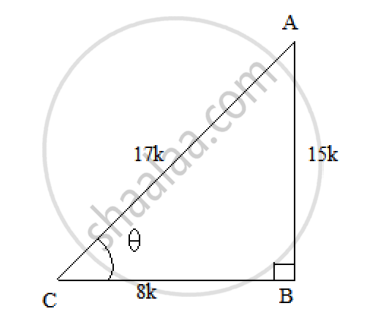
So, if BC = 8k, then AC = 17k, where k is a positive number.
Using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2`
`⟹ AB^2 = AC^2 − BC^2 = (17K)^2 − (8K)^2`
`⟹ AB^2 = 289K^2 − 64K^2 = 225K^2`
⟹AB = 15k.
Now, tan 𝜃 =`(AB)/(BC) =15/8 and sin theta =(AB)/(AC) =(15K)/(17K)=15/17`
The given expression is `(3-4 sin^2theta)/(4cos^2 theta-3) = (3-tan^2theta)/(1-3tan^2theta)`
Substituting the values in the above expression, we get:
LHS=`(3-4(15/17)^2)/(4(8/17)^2-3)`
=`(3-(900/289))/((250/289)-3)`
=`(867-900)/(256-867)=-33/-611 =33/611`
RHS = `(3-(15/8)^2)/(1-3(15/8)^2)`
= `(3-225/64)/(1-675/64)`
= `(192-255)/(64-675)=-33/-611 = 33/611`
∴ LHS = RHS
Hence proved.
APPEARS IN
संबंधित प्रश्न
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
Verify each of the following:
(iv) `2 sin 45^0 cos 45^0`
If A = 600 and B = 300, verify that:
cos (A + B) = cos A cos B - sin A sin B
If A = 600 and B = 300, verify that:
(ii) cos (A – B) = cos A cos B + sin A sin B
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cos A = `(7)/(25)`
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
