Advertisements
Advertisements
प्रश्न
If A = 600 and B = 300, verify that:
(ii) cos (A – B) = cos A cos B + sin A sin B
उत्तर
cos (A – B) = cos 300 =`sqrt(3)/2`
cos A cos B + sin A sin B = cos 600 cos 300 + sin 600 sin 300
=`( 1/2 xx sqrt(3)/2 + sqrt(3)/2 xx1/2) = (sqrt(3)/4 + sqrt(3)/4) = 2 xx sqrt(3)/4 = sqrt(3)/2`
∴ cos (A – B) = cos A cos B + sin A sin B
APPEARS IN
संबंधित प्रश्न
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

If A = 600 and B = 300, verify that:
cos (A + B) = cos A cos B - sin A sin B
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
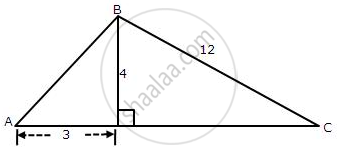
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cose C = `(15)/(11)`
If sinA = `(3)/(5)`, find cosA and tanA.
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
