Advertisements
Advertisements
प्रश्न
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
उत्तर
LHS = `((1-tan^2theta))/((1+tan^2theta))`
=` ((1-1/cot^2theta))/((1+1/cot^2theta))`
=`((cot^2theta-1)/(cot^2theta))/(((cot^2theta+1)/(cot^2theta)))`
=`(cot^2theta-1)/(cot^2theta+1)`
=`((4/3)^2-1)/((4/3)^2 +1)` (𝐴𝑠, 3 cot 𝜃 = 4 𝑜𝑟 cot 𝜃 =`4/3`)
=`(16/9-1)/(16/9+1)`
=`(((16-9)/9))/(((16+9)/9))`
=`((7/9))/((25/9))`
= `7/25`
𝑅𝐻𝑆 = `(cos^2 theta − sin^2 theta)`
=`((cos^2theta - sin^2 theta))/1`
=`(((cos^2theta-sin^2theta)/(sin^2theta)))/((1/(sin^2theta)))`
=`((cos^2theta)/(sin^2theta)-(sin^2theta)/(sin^2theta))/(cosec^2theta)`
=`((cot^2theta-1))/((cot^2theta+1))`
=`([(4/3)^2-1])/([(4/3)^2+1])`
=`((16/9-1/1))/((16/9+1/1))`
=`(((16-9)/9))/(((16+9)/9))`
=`((7/9))/((25/9))`
=`7/25`
Since, LHS = RHS
Hence, verified.
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
In right angled triangle ABC. ∠C = 90°, ∠B = 60°. AB = 15 units. Find remaining angles and sides.
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A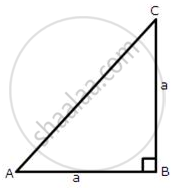
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: tan A
