Advertisements
Advertisements
प्रश्न
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A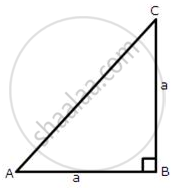
उत्तर
Given angle, ABC = 90° in the figure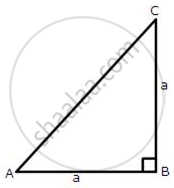
⇒ AC2 = AB2 + BC2 ...(AC is hypotenuse in Δ ABC )
⇒ AC2 = a2 + a2
∴ AC2 = 2a2 and AC =`sqrt2a`
Now
(i) sin A = `"perpendicular"/"hypotenuse" = "BC"/"AC" = a/(sqrt2a) = 1/(sqrt2)`
(ii) sec A = `"hypotenuse"/"base" = "AC"/"AB" = (sqrt2a)/a = sqrt2`
(iii) sin A = `"perpendicular"/"hypotenuse" = "BC"/"AC" = a/(sqrt2a) = 1/(sqrt2)`
cos A = `"base"/"hypotenuse" = "AB"/"AC" = a/(sqrt2a) = 1/(sqrt2)`
cos2A + sin2A = `(1/(sqrt2))^2 + (1 /(sqrt2))^2`
= `(1)/(2) +(1)/ (2)`
= 1
APPEARS IN
संबंधित प्रश्न
Given 15 cot A = 8. Find sin A and sec A.
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P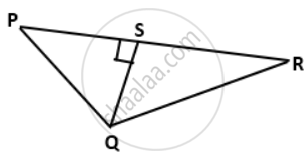
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
