Advertisements
Advertisements
प्रश्न
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
उत्तर
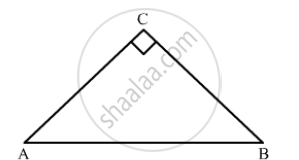
In ΔABC, ∠𝐶 = 90°
Tan A = `(BC)/(AC)` and
Tan B = `(AC)/(BC)`
As, tan 𝐴 = tan 𝐵
`⇒ (BC)/(AC) = (AC)/(BC)`
`⇒ BC^2 = AC^2`
⇒ BC=AC
So, ∠𝐴 = ∠𝐵 (𝐴𝑛𝑔𝑙𝑒𝑠 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑒𝑞𝑢𝑎𝑙 𝑠𝑖𝑑𝑒𝑠 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙)
APPEARS IN
संबंधित प्रश्न
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
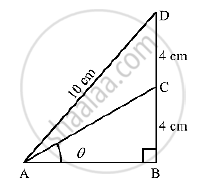
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
If tan x = `1(1)/(3)`, find the value of : 4 sin2x - 3 cos2x + 2
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
