Advertisements
Advertisements
प्रश्न
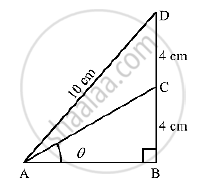
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
उत्तर
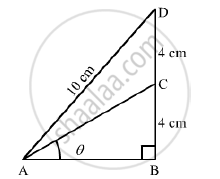
In ΔABD,
Using Pythagoras theorem, we get
AB= `sqrt(AD^2-BD^2)`
= `sqrt(10^2-8^2)`
=`sqrt(100-64)`
=`sqrt(36)`
=6cm
Again,
In ΔABC,
Using Pythagoras therem, we get
AC= `sqrt(AB^2 +BC^2)`
=`sqrt(6^2+4^2)`
=`sqrt(36+16)`
=`sqrt(52)`
=2`sqrt(13)`cm
Now,
(i) `sintheta = (BC)/(AC)`
=`4/(2sqrt(13))`
=`2/sqrt(13)`
=`(2 sqrt(13))/13`
(ii) `cos theta = (AB)/(AC)`
= `6/(2sqrt(13))`
=`3/sqrt(13)`
=`(3sqrt(13))/13`
APPEARS IN
संबंधित प्रश्न
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
In a ΔABC , ∠B = 90° , AB= 24 cm and BC = 7 cm find (i) sin A (ii) cos A (iii) sin C (iv) cos C
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
sin20° = cos ______°
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
If sinA = 0.8, find the other trigonometric ratios for A.
From the given figure, find the values of sec B