Advertisements
Advertisements
Question
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Solution
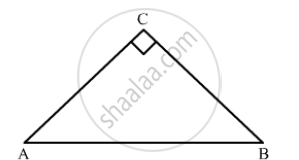
In ΔABC, ∠𝐶 = 90°
Tan A = `(BC)/(AC)` and
Tan B = `(AC)/(BC)`
As, tan 𝐴 = tan 𝐵
`⇒ (BC)/(AC) = (AC)/(BC)`
`⇒ BC^2 = AC^2`
⇒ BC=AC
So, ∠𝐴 = ∠𝐵 (𝐴𝑛𝑔𝑙𝑒𝑠 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑒𝑞𝑢𝑎𝑙 𝑠𝑖𝑑𝑒𝑠 𝑎𝑟𝑒 𝑒𝑞𝑢𝑎𝑙)
APPEARS IN
RELATED QUESTIONS
If 𝜃 = 30° verify `cos 2 theta = (1 - tan^2 theta)/(1 + tan^2 theta)`
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If ∠A and ∠B are acute angles such that sin A = Sin B prove that ∠A = ∠B.
Evaluate:
`(sin^2 30^0 + 4 cot^2 45^0-sec^2 60^0)(cosec^2 45^0 sec^2 30^0)`
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
If cos A = `(1)/(2)` and sin B = `(1)/(sqrt2)`, find the value of: `(tan"A" – tan"B")/(1+tan"A" tan"B")`.
Are angles A and B from the same triangle? Explain.
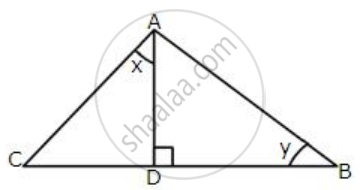
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
