Advertisements
Advertisements
Question
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
Solution
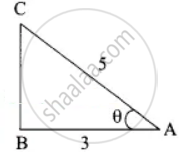
cos A = `3/5`
ΔABC
BC2 = AC2 – AB2
= 52 – 32
= 25 – 9
= 16
BC = `sqrt(16)` = 4
sin A = `4/5`, tan A = `4/3`
`(sin"A" - cos"A")/(2tan"A") = 4/5 - 3/5 ÷ 2(4/3)`
= `(4 - 3)/5 ÷(8/3)`
= `1/5 xx (3/8)`
= `3/40`
∴ The value of `(sin"A" - cos"A")/(2tan"A") = 3/40`
APPEARS IN
RELATED QUESTIONS
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
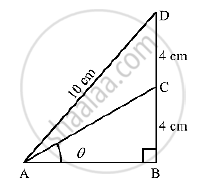
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
If cos A = `(1)/(2)` and sin B = `(1)/(sqrt2)`, find the value of: `(tan"A" – tan"B")/(1+tan"A" tan"B")`.
Are angles A and B from the same triangle? Explain.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
