Advertisements
Advertisements
Question
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
Solution
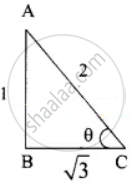
2 cos θ = `sqrt(3)`
⇒ cos θ = `sqrt(3)/2`
AB2 = AC2 – BC2
= `2^2 - (sqrt(3))^2`
⇒ 4 – 3 = 1
AB = `sqrt(1)` = 1
sin θ = `"opposite side"/"hypotenuse" = 1/2`
cos θ = `"adjacent side"/"hypotenuse" = sqrt(3)/2`
tan θ = `"opposite side"/"adjacent side" = 1/sqrt(3)`
cosec θ = `"hypotenuse"/"opposite side"` = 2
sec θ = `"hypotenuse"/"adjacent side" = 2/sqrt(3)`
cot θ = `"adjacent side"/"opposite side" = sqrt(3)`
APPEARS IN
RELATED QUESTIONS
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: sinB
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
From the given figure, find the values of cosec C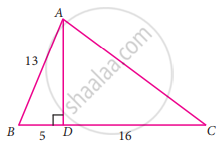
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
