Advertisements
Advertisements
Question
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
Solution
sin (A-B)= sin `30^0 = 1/2`
sin A cos B - cos A sin B = sin `60^0 cos 30^0 - cos 60^0 sin 30^0`
=` (sqrt(3)/2 xx sqrt(3)/2 - 1/2 xx1/2 ) =(3/4 - 1/4) = 2/4 =1/2`
∴ sin (A – B) = sin A cos B – cos A sin B
APPEARS IN
RELATED QUESTIONS
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
If sin A = `9/41` find all the values of cos A and tan A
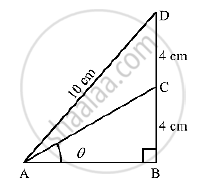
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
