Advertisements
Advertisements
प्रश्न
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
उत्तर
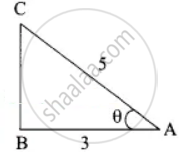
cos A = `3/5`
ΔABC
BC2 = AC2 – AB2
= 52 – 32
= 25 – 9
= 16
BC = `sqrt(16)` = 4
sin A = `4/5`, tan A = `4/3`
`(sin"A" - cos"A")/(2tan"A") = 4/5 - 3/5 ÷ 2(4/3)`
= `(4 - 3)/5 ÷(8/3)`
= `1/5 xx (3/8)`
= `3/40`
∴ The value of `(sin"A" - cos"A")/(2tan"A") = 3/40`
APPEARS IN
संबंधित प्रश्न
If θ = 30° verify that `sin 2theta = (2 tan theta)/(1 + tan^2 theta)`
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
If A = 600 and B = 300, verify that:
(iii) tan (A-B) = `(tan A-tanB)/(1+tan A tan B)`
Using the formula, sin A = `sqrt((1-cos 2A)/2) ` find the value of sin 300, it being given that cos 600 = `1/2`
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: cos C
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
