Advertisements
Advertisements
प्रश्न
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
उत्तर
On substituting the values of various T-ratios, we get:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
=`2xx(1/2)^2 + 3 xx(1/sqrt(2))^2 -3 xx (1/2)^2 + 2 xx (0)^2`
=`2xx1/4+3xx1/2-3xx1/4+0`
=`(1/2 +3/2-3/4)=((2+6-3)/4)=5/4`
APPEARS IN
संबंधित प्रश्न
Given 15 cot A = 8. Find sin A and sec A.
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
Given : 5 cos A - 12 sin A = 0; evaluate:
`(sin "A"+cos"A")/(2 cos"A"– sin"A")`
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y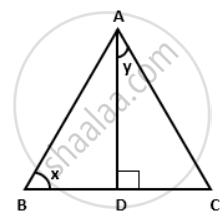
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
