Advertisements
Advertisements
Question
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
Solution
On substituting the values of various T-ratios, we get:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
=`2xx(1/2)^2 + 3 xx(1/sqrt(2))^2 -3 xx (1/2)^2 + 2 xx (0)^2`
=`2xx1/4+3xx1/2-3xx1/4+0`
=`(1/2 +3/2-3/4)=((2+6-3)/4)=5/4`
APPEARS IN
RELATED QUESTIONS
In rectangle ABCD AB = 20cm ∠BAC = 60° BC, calculate side BC and diagonals AC and BD.
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
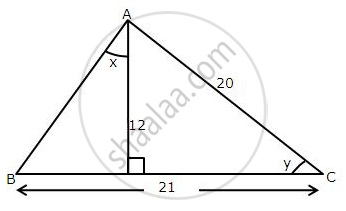
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
