Advertisements
Advertisements
Question
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
Solution
sinA = `(12)/(13)`
sinA = `"Perpendicular"/"Hypotenuse" = (12)/(13)`
By Pythagoras theorem, we have
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ Base = `sqrt(("Hypotenuse")^2 - ("Perpendicular")^2`
⇒ Base
= `sqrt((13)^2 - (12)^2`
= `sqrt(169 - 144)`
= `sqrt(25)`
= 5
cosA = `"Base"/"Hypotenuse" = (5)/(13)`
secA = `(1)/"cosA" = (13)/(5)`
cotA = `(1)/"tanA" = (5)/(12)`
cosecA = `(1)/"sinA" = (13)/(12)`.
APPEARS IN
RELATED QUESTIONS
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of sin A sin B + cos A cos B
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
If sin θ = `3/4` show that `sqrt((cosec^2theta - cot^2theta)/(sec^2theta-1)) =sqrt(7)/3`
Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cosec C
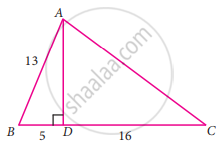
From the given figure, find the values of cot B