Advertisements
Advertisements
Question
Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
Solution
On substituting the values of various T-ratios, we get:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
=`(sqrt(3))^2 - 2 xx(sqrt(3)/2)^2 - 3/4 xx(sqrt(2))^2+1/4xx(2)^2`
=`3-2xx3/4-3/4xx2+1/4xx4`
=`3-3/2-3/2+1`
=`4-(3/2+3/2)`
`=4-3=1`
APPEARS IN
RELATED QUESTIONS
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
Evaluate:
sin600 cos300 + cos600 sin300
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y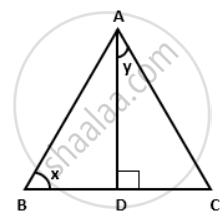
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
