Advertisements
Advertisements
Question
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
Solution
cos θ = `(3)/(5)`
Now
`(co secθ – cot θ)/(co secθ + cot θ) = (1/sinθ – cosθ/sinθ)/(1/ sinθ + cosθ/sinθ)`
= `((1 – cos θ)/(sin θ))/((1 + cos θ)/(sinθ))`
= `( 1 – cos θ)/(1 + cos θ)`
= `(1 – (3)/(5))/(1+(3)/(5))`
= `((2)/(5))/((8)/(5))`
= `(2)/(8)`
= `(1)/(4)`
APPEARS IN
RELATED QUESTIONS
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
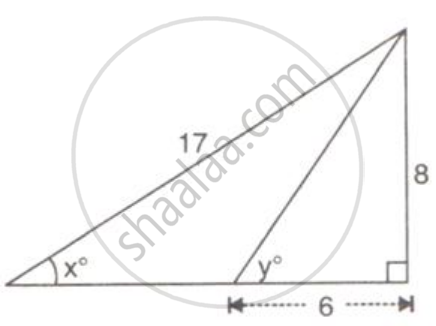
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
