Advertisements
Advertisements
Question
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
Solution
Let us consider a right ΔABC, right angled at B and ∠𝐶 = 𝜃.
Now, it is given that cosec θ = 2.
Also , sin θ ` = 1/(cosecθ) = 1/2 = (AB)/(AC)`
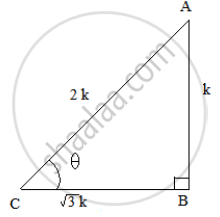
So, if AB =k, then AC =2k, where k is a positive number.
Using Pythagoras theorem, we have:
`⟹ AC^2 = AB^2 + BC^2`
`⟹ BC^2 = AC^2 − AB^2`
`⟹ BC^2 (2K)^2 − (K)^2`
`⟹ BC^2 = 3K^2`
`⟹ BC = sqrt(3k)`
Finding out the other T-ratios using their definitions, we get:
`cos θ = (BC)/(AC) = (sqrt(3k))/(2k) = (sqrt(3))/2`
`tan θ = (AB)/(BC) = K/(sqrt(3k)) = 1/(sqrt(3))`
`Cot θ = 1/ (tan θ) = sqrt(3)`
Substituting these values in the given expression, we get:
cot θ +`(sin θ)/(1+cos θ)`
`= sqrt(3)+((1/2))/(1+sqrt(3)/2`
=`sqrt(3) + (1/2)/((2+sqrt(3))/2)`
=`sqrt(3) + 1/(2+sqrt(3)`
=`(sqrt(3)(2+sqrt(3)+1))/(2+sqrt(3))`
=`(2sqrt(3)+3+1)/(2+sqrt(3)`
=` (2(2+sqrt(3)))/(2+sqrt(3))=2`
i.e., LHS = RHS
Hence proved.
APPEARS IN
RELATED QUESTIONS
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
If θ = 30° verify that `sin 2theta = (2 tan theta)/(1 + tan^2 theta)`
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
Evaluate:
sin600 cos300 + cos600 sin300
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm.
find :
- tan ∠DBC
- sin ∠DBA

In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P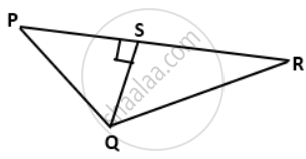
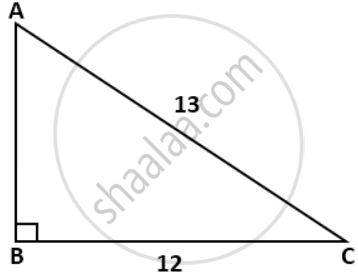
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A