Advertisements
Advertisements
प्रश्न
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
उत्तर
Let us consider a right ΔABC, right angled at B and ∠𝐶 = 𝜃.
Now, it is given that cosec θ = 2.
Also , sin θ ` = 1/(cosecθ) = 1/2 = (AB)/(AC)`
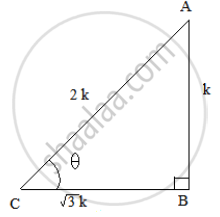
So, if AB =k, then AC =2k, where k is a positive number.
Using Pythagoras theorem, we have:
`⟹ AC^2 = AB^2 + BC^2`
`⟹ BC^2 = AC^2 − AB^2`
`⟹ BC^2 (2K)^2 − (K)^2`
`⟹ BC^2 = 3K^2`
`⟹ BC = sqrt(3k)`
Finding out the other T-ratios using their definitions, we get:
`cos θ = (BC)/(AC) = (sqrt(3k))/(2k) = (sqrt(3))/2`
`tan θ = (AB)/(BC) = K/(sqrt(3k)) = 1/(sqrt(3))`
`Cot θ = 1/ (tan θ) = sqrt(3)`
Substituting these values in the given expression, we get:
cot θ +`(sin θ)/(1+cos θ)`
`= sqrt(3)+((1/2))/(1+sqrt(3)/2`
=`sqrt(3) + (1/2)/((2+sqrt(3))/2)`
=`sqrt(3) + 1/(2+sqrt(3)`
=`(sqrt(3)(2+sqrt(3)+1))/(2+sqrt(3))`
=`(2sqrt(3)+3+1)/(2+sqrt(3)`
=` (2(2+sqrt(3)))/(2+sqrt(3))=2`
i.e., LHS = RHS
Hence proved.
APPEARS IN
संबंधित प्रश्न
If 𝜃 = 30° verify `cos 2 theta = (1 - tan^2 theta)/(1 + tan^2 theta)`
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
If cot θ = `3/4` , show that `sqrt("sec θ - cosecθ"/"secθ + cosecθ" ) = 1/ sqrt(7)`
If ∠A and ∠B are acute angles such that sin A = Sin B prove that ∠A = ∠B.
Verify each of the following:
(iv) `2 sin 45^0 cos 45^0`
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
