Advertisements
Advertisements
प्रश्न
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
उत्तर
Sin(A + B) = 1
∴ Sin (A + B) = Sin 90°
A + B = 90° …(i)
Cos (A – B) = 1
Cos (A – B) = cos 0°
A – B = 0° …(ii)
Adding (i) and (ii) we get
A + B = 90°
`(A - B = 0^@)/(A = 90^@)` `A = 45^@`
A – B = 0
A = B => B = 45°
APPEARS IN
संबंधित प्रश्न
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
Evaluate:
cos450 cos300 + sin450 sin300
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ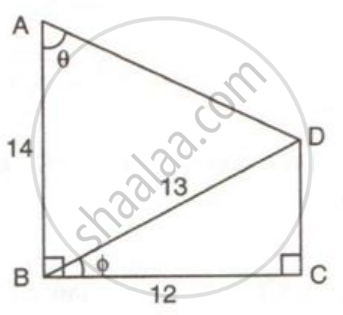
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
