Advertisements
Advertisements
प्रश्न
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
उत्तर
LHS = `((sin theta - cot theta ))/(2tantheta)`
=`(sin theta costheta /sintheta )/(2(sintheta/costheta))`
=`((sin^2theta - costheta)/sintheta)/((2 sintheta/costheta))`
=` (costheta(sin^2theta-costheta))/(2sin^2theta)`
=`(costheta (1-cos^2theta-costheta))/(2(1-cos^2theta))`
=`(3/5[1-(3/5)^2-3/5])/(2[1-(3/5)^2])`
=`(3/5(1/1-9/25-3/5))/(2(1-9/25))`
=`(3/5((25-9-15)/25))/(2((25-9)/25))`
=`(3/5(1/25))/(2(16/25))`
=`3/(5xx2xx16)`
=`3/160`
= RHS
APPEARS IN
संबंधित प्रश्न
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
If sin A = `9/41` find all the values of cos A and tan A
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
Evaluate:
sin600 cos300 + cos600 sin300
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
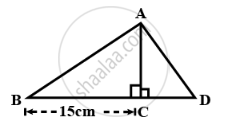
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
