Advertisements
Advertisements
प्रश्न
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
उत्तर
We have to prove: `cos[(B+C)/2] = sin A/2`
Since we know that in triangle ABC
`A + B + C = 180^@`
`=> B + C = 180^@ - A`
Dividing by 2 on both sides, we get
`=> (B +C)/2 = 90^@ - A/2`
`=> cos (B + C)/2 = cos (90^@ - A/2)`
`=> cos (B + C)/2 = sin A/2`
Proved
APPEARS IN
संबंधित प्रश्न
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`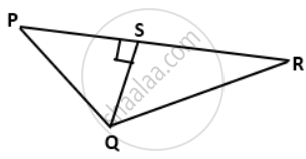
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
