Advertisements
Advertisements
प्रश्न
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
उत्तर
cos θ = `(3)/(5)`
Now
`(co secθ – cot θ)/(co secθ + cot θ) = (1/sinθ – cosθ/sinθ)/(1/ sinθ + cosθ/sinθ)`
= `((1 – cos θ)/(sin θ))/((1 + cos θ)/(sinθ))`
= `( 1 – cos θ)/(1 + cos θ)`
= `(1 – (3)/(5))/(1+(3)/(5))`
= `((2)/(5))/((8)/(5))`
= `(2)/(8)`
= `(1)/(4)`
APPEARS IN
संबंधित प्रश्न
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If A = 30° B = 60° verify Sin (A + B) = Sin A Cos B + cos A sin B
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
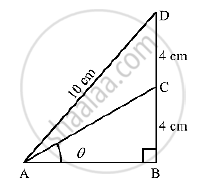
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
tan 30° × tan ______° = 1
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
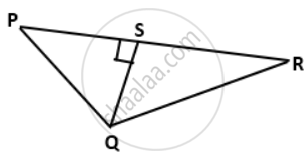
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P