Advertisements
Advertisements
प्रश्न
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
उत्तर
Let us first draw a right ΔABC, right angled at B and ∠𝐶 = 𝜃
Now, we know that tan θ = `"𝑃𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟"/" 𝐵𝑎𝑠𝑒"=(AB)/(BC) = 15/8`
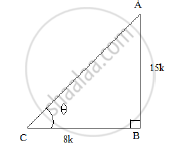
So, if BC = 8k, then AB = 15k where k is positive number.
Now, using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2 = (15K)^2 + (8K)^2`
`⟹ AC^2 = 225K^2 + 64^2 = 289^2`
⟹ AC = 17k
Now, finding the other T-ratios using their definitions, we get:
Sin 𝜃 = `(AB)/(AC) = (15 K)/(17K) = 15/17`
Cos θ = `(BC)/(AC) = (8K)/(17K) = 8/17`
∴ cot 𝜃 = `1/(tan θ ) = 8/15 , cosec θ = 1/(sin θ ) = 17/15 and sec θ = 1/(cos θ ) = 17/8`
APPEARS IN
संबंधित प्रश्न
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
Verify each of the following:
(iv) `2 sin 45^0 cos 45^0`
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosB = `(4)/(5)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
From the given figure, find the values of cosec C