Advertisements
Advertisements
प्रश्न
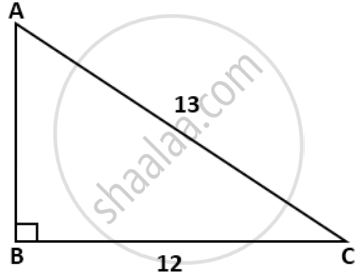
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
उत्तर
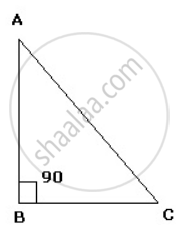
In ΔABC,
AC2 = AB2 + BC2
⇒ AC = `sqrt("AB"^2 + "BC"^2)`
⇒ AC = `sqrt(12^2 + 5^2)`
= `sqrt(144 + 25)`
= 13
AB = 12units
BC = 5units
AC = 13units
cos C
= `"Base"/"Hypotenuse"`
= `"BC"/"AC"`
= `(5)/(13)`.
APPEARS IN
संबंधित प्रश्न
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A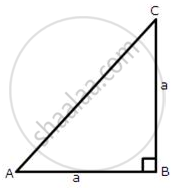
If cot θ= 1; find the value of: 5 tan2 θ+ 2 sin2 θ- 3
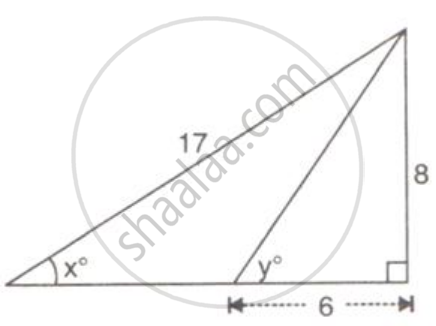
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A