Advertisements
Advertisements
प्रश्न
If cos θ = `7/25` find the value of all T-ratios of θ .
उत्तर
Let us first draw a right ΔABC, right angled at B and ∠𝐶 = 𝜃.
Now, we know that cos 𝜃 = `"𝐵𝑎𝑠𝑒" /"ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠" = (BC)/(AC) = 7/25`
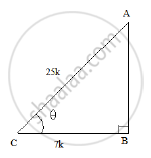
So, if BC = 7k, then AC = 25k, were k is a positive number.
Now, using Pythagoras theorem, we have:
`AC^2= AB^2 + BC^2`
`⟹ AB^2 = AC^2 − BC^2 = (25K)^2 − (7K)^2`
`⟹ AB^2 = 625K^2 − 49K^2 = 576^2`
⟹ AB = 24k
Now, finding the trigonometric ratios using their definitions, we get:
Sin 𝜃 =` (AB)/(AC) = (24K)/(25K) = 24/25`
Sin 𝜃 =`(AB)/(BC) = (24K)/(7K) = 24/7`
∴ cot 𝜃 = `1/ (tan θ) = 7/24 , cosec θ = 1/(sin θ) = 25/24 and sec θ = 1/ (cos θ) = 25/7`
APPEARS IN
संबंधित प्रश्न
Given 15 cot A = 8. Find sin A and sec A.
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A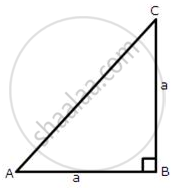
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
If 5 cot θ = 12, find the value of : Cosec θ+ sec θ
If cosec θ = `sqrt5`, find the value of:
- 2 - sin2 θ - cos2 θ
- 2 + `1/sin^2"θ" – cos^2"θ"/sin^2"θ"`
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm.
find :
- tan ∠DBC
- sin ∠DBA

In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: sinA
