Advertisements
Advertisements
प्रश्न
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
उत्तर
We have
`sin theta = 3/5`
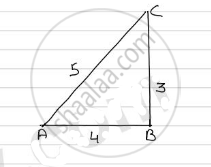
In Δ ABC
`AC^2 = AB^2 + BC^2`
`=> (5)^2 = (3)^2 + (BC)^2`
`=> 25 = 9 + (BC)^2`
`=> (BC)^2 = 25 - 9`
=> (BC)^2 = 16
=> BC = 4
`:. cos theta = 4/5 and cot theta = 4/3`
Now `(cos theta - 1/(tan theta))/(2 cot theta) = ((4/5) - (4/3))/(2 xx 4/3)`
`= ((12 - 20)/15)/(8/3)`
`= (-8)/15 xx 3/8`
`= (-1)/5`
APPEARS IN
संबंधित प्रश्न
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
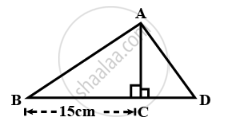
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
In triangle ABC, ∠B = 90° and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
From the given figure, find the values of cosec C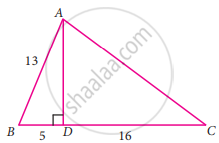
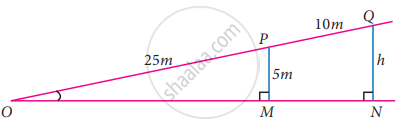
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)