Advertisements
Advertisements
प्रश्न
if `sec A = 5/4` verify that `(3 sin A - 4 sin^3 A)/(4 cos^3 A - 3 cos A) = (3 tan A - tan^3 A)/(1- 3 tan^2 A)`
उत्तर
We have
`sec A = 5/4`

In ΔABC
`AC^2 = AB^2 + BC^2`
`=> (5)^2 = (4)^2 + (BC)^2`
`=> BC^2 = 25 - 16`
=> BC = 3
`sin A = 3/5, cos A = 4/5 and tan A = 3/4`
Now
`(3sin A - 4sin^3 A)/(4 cos^3 A - 3 cosA) = (3 tan A - tan^3 A)/(1 - 3tan^2 A)`
`=> (3 xx 3/5 - 4 xx (3/5)^2)/(4 xx (4/5)^3 - 3 xx (4/5)) = (3xx (3/4) - (3/4)^3)/(1 - 3xx(3/4)^2)`
`=> (9/5 - 108/125)/(256/25 - 12/5) = (9/4 - 27/64)/(1 - 27/16)`
`=> ((225 - 108)/125)/((256 - 300)/125) = ((144 - 27)/64)/((16 - 27)/16)`
`=> 117/(-44) = 117/(-11xx4)`
=> L.H.S = R.H.S
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
In triangle ABC, ∠B = 90° and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: tan B.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
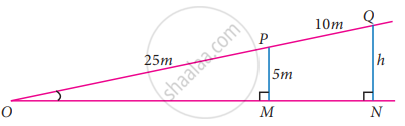
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)