Advertisements
Advertisements
प्रश्न
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
उत्तर
In the ΔABC,
AB = 9 + 16 = 25
AC = 15, BC = 20
AB2 = 252
= 625 ...(1)
AC2 + BC2 = 152 + 202
= 225 + 400
= 625 ...(2)
From (1) and (2) we get
AB2 = AC2 + BC2
ABC is a right angle triangle at C ...(Pythagoras theorem)
∴ ∠C = 90°
θ + ∅ = 90°
Also ADC is a right angle triangle ∠ADC = 90° ...(Given)
BDC is also a right angle triangle ∠BDC = 90° ...(since ADB is a straight line sum of the two angle is 180°)
From the given diagram
sin α = `"DC"/"AC" = 12/15 = 4/5`
cos β = `"BD"/"BC" = 16/20 = 4/5`
tan Φ = `"BD"/"CD" = 16/12 = 4/3`
APPEARS IN
संबंधित प्रश्न
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A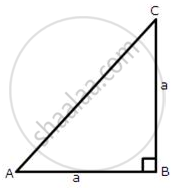
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
If sinA = `(3)/(5)`, find cosA and tanA.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P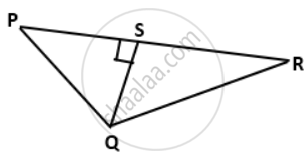
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
