Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If `sin A = 9/41` compute cos ЁЭР┤ ЁЭСОЁЭСЫЁЭСС tan ЁЭР┤
рдЙрддреНрддрд░
`sin A = 9/41`
`sin A = "ЁЭСЬЁЭСЭЁЭСЭЁЭСЬЁЭСаЁЭСЦЁЭСбЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ"/"ЁЭСОЁЭССЁЭСЧЁЭСОЁЭСРЁЭСТЁЭСЫЁЭСб ЁЭСаЁЭСЦЁЭССЁЭСТ" = 9/41`
Consider the right-angled triangle ABC,
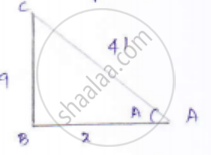
Let x be the adjacent side
By applying Pythagorean
ЁЭР┤ЁЭР╢2 = ЁЭР┤ЁЭР╡2 + ЁЭР╡ЁЭР╢2
412 = 122 + 92
ЁЭСе2 = 412 − 92
ЁЭСе = 40
`cos A = "ЁЭСОЁЭССЁЭСЧЁЭСОЁЭСРЁЭСТЁЭСЫЁЭСб ЁЭСаЁЭСЦЁЭССЁЭСТ"/"тДОЁЭСжЁЭСЭЁЭСЬЁЭСбЁЭСТЁЭСЫЁЭСвЁЭСаЁЭСТ" = 40/41`
`tan A = "ЁЭСЬЁЭСЭЁЭСЭЁЭСЬЁЭСаЁЭСЦЁЭСбЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ"/"ЁЭР╗ЁЭСжЁЭСЭЁЭСЬЁЭСбЁЭСТЁЭСЫЁЭСвЁЭСаЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ" = 9/40`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
If cos A = `(1)/(2)` and sin B = `(1)/(sqrt2)`, find the value of: `(tan"A" – tan"B")/(1+tan"A" tan"B")`.
Are angles A and B from the same triangle? Explain.
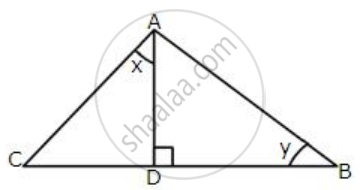
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
