Advertisements
Advertisements
Question
If `sin A = 9/41` compute cos ๐ด ๐๐๐ tan ๐ด
Solution
`sin A = 9/41`
`sin A = "๐๐๐๐๐ ๐๐ก๐ ๐ ๐๐๐"/"๐๐๐๐๐๐๐๐ก ๐ ๐๐๐" = 9/41`
Consider the right-angled triangle ABC,
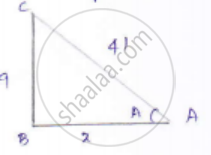
Let x be the adjacent side
By applying Pythagorean
๐ด๐ถ2 = ๐ด๐ต2 + ๐ต๐ถ2
412 = 122 + 92
๐ฅ2 = 412 − 92
๐ฅ = 40
`cos A = "๐๐๐๐๐๐๐๐ก ๐ ๐๐๐"/"โ๐ฆ๐๐๐ก๐๐๐ข๐ ๐" = 40/41`
`tan A = "๐๐๐๐๐ ๐๐ก๐ ๐ ๐๐๐"/"๐ป๐ฆ๐๐๐ก๐๐๐ข๐ ๐ ๐ ๐๐๐" = 9/40`
APPEARS IN
RELATED QUESTIONS
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
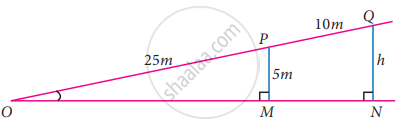
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)
